PCA原理 这里 。
LDA原理
详细推导步骤参考PRML4.1.4 P186,或者这里
补充1
\begin{equation} S_W^{-1}S_Bu=S_W^{-1}c(m_1-m_2)=\lambda u\end{equation}
则可以直接求出u为
补充2 矩阵的协方差 ,其计算方法是:
所以求矩阵的的协方差可以先将样本进行中心化,然后乘以其转置矩阵。则X的协方差为
在matlab中使用PCA
COEFF是X矩阵所对应的协方差阵V的所有特征向量组成的矩阵,即变换矩阵或称投影矩阵。(principal component coefficients)
一般的话,当percent达到90%以上我们认为属于符合要求的。
详见:matlab官网
在matlab中使用LDA
sample是需要分类的数据,training是训练的数据,group是分组信息,class是预测的标签。由此可见sample必须和training有相同的列数,因为维度必须相同。training和group必须行数相同,因为每个元素要分一类。
详见:matlab官网
Please enable JavaScript to view the comments powered by Disqus.
comments powered by
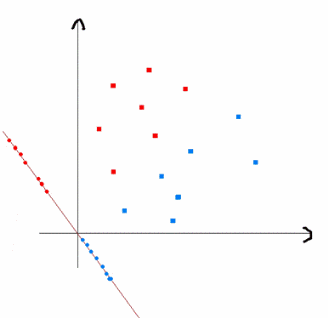 而该问题是优化如下问题:
而该问题是优化如下问题: