前段时间看《编程之美》,看到一个问题“如何精确表示浮点数”。看了一下书中的解答,感觉有问题,贴出来给大家看下
>在计算机中,使用float或者double来存储小数是不能得到精确值的。如果你希望得到精确计算结果,最好是用分数形式来表示小数。有限小数或者无限循环小数都可以转化为分数。比如:
>0.9 = 9/10
>0.333(3)= 1/3(括号中的数字表示是循环节)
>当然一个小数可以用好几种分数形式来表示。如:
>0.333(3)= 1/3 = 3/9
>给定一个有限小数或者无限循环小数,你能否以分母最小的分数形式来返回这个小数呢?如果输入为循环小数,循环节用括号标记出来。下面是一些可 能的输入数据,如0.3、0.30、0.3(000)、0.3333(3333)、……

 看完后,我的第一感觉就是作者的语文课是体育老师教的吧,等到细读之后才发现,敢情数学课也是体育老师教的。
看完后,我的第一感觉就是作者的语文课是体育老师教的吧,等到细读之后才发现,敢情数学课也是体育老师教的。
其实这个问题的关键就是在于无限循环小数的处理,看书中的处理
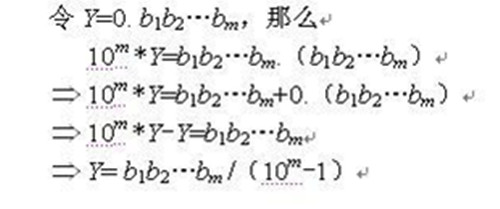 这不是扯淡吗,你只考虑了循环两位的情况,就求出Y的推导公式?!我想说,虽然你的结果是正确的,可是这逻辑实在没法让人信服。
然后更搞笑的是它的X推导式,最后的结果分母上居然还有参数n,如果是无限循环,n取到无穷大,那X不就是零了嘛,面对如此编书的,我只想说,呵呵。
这不是扯淡吗,你只考虑了循环两位的情况,就求出Y的推导公式?!我想说,虽然你的结果是正确的,可是这逻辑实在没法让人信服。
然后更搞笑的是它的X推导式,最后的结果分母上居然还有参数n,如果是无限循环,n取到无穷大,那X不就是零了嘛,面对如此编书的,我只想说,呵呵。
那么正确的方法应该是什么呢
对于任意一个无限循环的浮点数,都可以这样表示
\begin{equation}0.(b_1b_2…b_m)=(b_1b_2…b_m)\times (\frac{1}{10^m}+\frac{1}{100^m}+\frac{1}{1000^m}…\frac{1}{10^{nm}})\end{equation}
可见等式右侧的后半部分是一个几何级数,根据几何级数的敛散性,这个是收敛级数,而当n趋近于无穷大时,该级数收敛于
\begin{equation}\frac{a_1}{1-q}=\frac{\frac{1}{10^m}}{1-\frac{1}{10^m}}=\frac{1}{10^m-1}\end{equation}
那么
\begin{equation}0.(b_1b_2…b_m)=(b_1b_2…b_m)\frac{1}{10^m-1}\end{equation}
可以带入书中的例子试下,当m=1,小数部分为3时,以及m=6,小数部分为285714时。最后再次吐槽下该书,你看他最后的例子计算,居然把n等于6,才凑出了正确答案,我只想说,哈哈哈
comments powered by

 看完后,我的第一感觉就是作者的语文课是体育老师教的吧,等到细读之后才发现,敢情数学课也是体育老师教的。
看完后,我的第一感觉就是作者的语文课是体育老师教的吧,等到细读之后才发现,敢情数学课也是体育老师教的。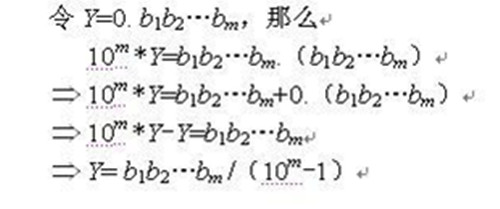 这不是扯淡吗,你只考虑了循环两位的情况,就求出Y的推导公式?!我想说,虽然你的结果是正确的,可是这逻辑实在没法让人信服。
然后更搞笑的是它的X推导式,最后的结果分母上居然还有参数n,如果是无限循环,n取到无穷大,那X不就是零了嘛,面对如此编书的,我只想说,呵呵。
这不是扯淡吗,你只考虑了循环两位的情况,就求出Y的推导公式?!我想说,虽然你的结果是正确的,可是这逻辑实在没法让人信服。
然后更搞笑的是它的X推导式,最后的结果分母上居然还有参数n,如果是无限循环,n取到无穷大,那X不就是零了嘛,面对如此编书的,我只想说,呵呵。