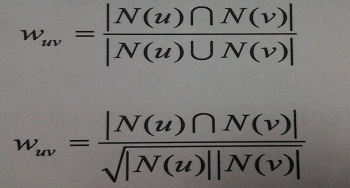
最近读了《推荐系统实战》,这本书干货不多,不过我是从图书馆借的书,又没花钱,所以没有吐槽的动力,倒是花了很短的时间读了一本书,反而感觉很有成就感,嘿嘿。
最基本的推荐方法就是使用K近邻方法,而K近邻又分成基于用户的协同过滤算法和基于物品的协同过滤算法。根据用户的协同过滤算法,其原理就是找到与用户最相似的人,然后推荐那个人的物品清单中,该用户没有的物品。而度量用户的相似度,就是度量两个用户清单中相同元素所占的比例。实际操作中可以用Jaccard相似系数或者是余弦相似度,
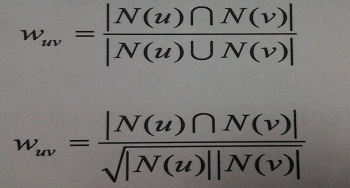
下面看一个具体的例子,都是计算余弦相似度的,分母表示两个元素组个数之积,Jaccard相似系数比较简单,这里不再赘述,
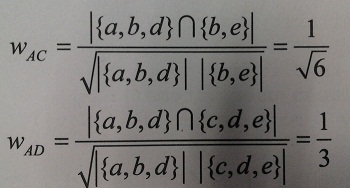
这样一来,所有问题看起来变得都非常简单了,如果我们要给A推荐物品,就把A和所有的用户计算相似度,然后选取前K个相似度最大的用户,把这些用户列表中A没有的物品推荐给A就行了。可是这样做会有一个问题,就是大部分用户和A都没有共同的兴趣,这样我们就会大量的时间浪费在计算相似度为零上。为了解决这个问题,我们实际操作时,往往先建立一个元素到用户的倒查表,再根据这个表来统计各个用户之间的相似度,如图
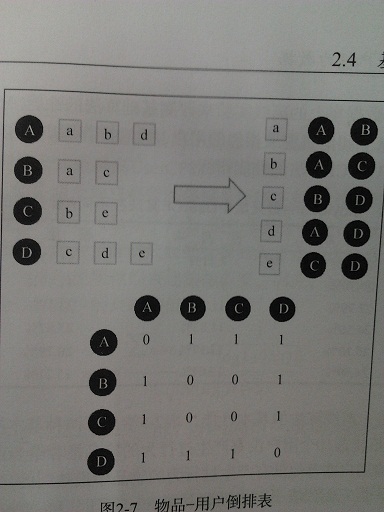
对于元素a,它的用户表是A,B。那么就把AB置为1。元素b的用户表是A,C。那么就把AC置为1,以此类推。(如果此时b的用户表是A,B的话,此时AB置为2)
这个矩阵是一个对角阵,每个元素是两个用户之间的共同兴趣,比如要计算上图中A和D的余弦相似度,查的A行D列的元素是1,然后看A列的元素个数是3,D列元素个数是3,则AB的余弦相似度是1/3。(这里省略9开根号)
现在已经可以很容易的找到用户A的最相似的用户,那么实际操作中如何给A推荐物品呢。我们使用上图中的例子,选择K为3,选择Jaccard相似系数来表示相似度。由上图可知,离A最近的元素是B,C,D,然后A中没有的元素是c,e。则需要把这两个推荐给A,那么A与c的相似度与A与e的相似度哪个更高呢?
similarity(A,c)=similarity(A,B)*similarity(B,c)+similarity(A,D)*similarity (D,c)
=1/4 *1+1/5*1
=9/20
similarity(A,e)=similarity(A,C)*similarity(C,e)+similarity(A,D)*similarity (D,e)
=1/4 *1+1/5*1
=9/20
这里由于题目中没有给出用户对用户列表中每个元素具体的兴趣,所以我们默认用户对自己列表中的物品的兴趣都是1,所以similarity(B,c)等等都设置为1。
最后还有一个问题,就是如果一个物品特别热门,那么几乎每个用户中都这个物品,那么计算两个用户相似度时就会不那么”准“,所以我们实际操作时往往还要对热门的物品加个惩罚项。
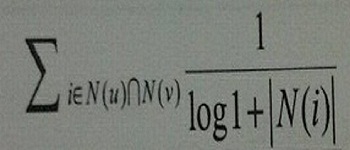
这里N(i)表示,对物品i有过行为的用户集合。
以上是基于用户的协同过滤算法的简单阐述,基于物品的协同过滤算法使用同样的方法,如果用一个词来总结的话,就是vice versa,哈哈。不同的是基于物品的协同过滤算法度量物品的相似度,比较的是两个物品的用户列表,于是统计用户相似度时,也要建立一张用户物品的倒查表。基于物品的协同过滤算法的惩罚项是热门度最高的人,如果一个人对所有的物品都有过行为,我们就不认为这个人对度量两个物品相似度有较小的影响。
那么什么时候使用user-based什么时候使用item-based呢?user-based主要应用于用户数基本不变,而物品经常变化的情况,如新闻网站。user-based更倾向于表达用户之间的兴趣。而item-based主要应用于物品不变,用户经常变化的情况,如果亚马逊。item-based更倾向于表达用户的历史喜好。
再一个就是关于LFM( Latent Factor Mode)的东西,这个东西和矩阵分解有着千丝万缕的关系,包括SVD什么的,由于实在没有时间,我这里就简单截个书中的图,看公式也很容易理解,等日后在写个矩阵分解的专题。

此外,书中还有几章关于冷启动,用户标签,上下文信息,社交网络数据的内容,个人感觉营养不高,所以这里不在记录,不过作为小品文,算是对推荐系统的一个了解也是很不错的。