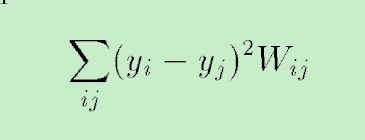
在古代的时候,牛人写一本书,总会有后人来对这本书来进行注解,比如《老子》,《庄子》甚至是《全唐诗》历朝历代都会有各种版本的注本。为什么会出现这种情况呢,估计是因为我们常人太平庸了,无法理解这些书的精妙之处,所以需要一些人来给我们讲解。可是当我们的水平慢慢提高以后,能够独自揣摩作者的意图后,就不需要这些注解的书。有的时候这些注解的书甚至会成为一种障碍,对你的思想形成一种限制。比如读《老子》时,我的老师就不建议我读南怀瑾的《老子他说》,他说有些道理你必须自己去领悟,确实我读书时就有很多与南老师不同的见解,而我也更愿意相信自己的观点。
读哲学类的书不解往往是因为我们生活阅历太浅,而读科学类的书时不解大多是因为我们数学基础薄弱,当我在学习Laplacian Eigenmap和 Spectral Clustering时,看到这一大堆公式感到非常的不解,甚至怀疑作者写的太烂。可是当我认真坐下来,把所有公式推导一遍后,发现作者写的实在是太经典了,堪称完美的经典。
以下我将罗列每个公式的缘由,作为学习这部分的学习笔记。
Laplacian Eigenmap问题关键就是最优化这个公式,(如果你不懂为什么,建议你去先看文章结尾的reference里的文章)
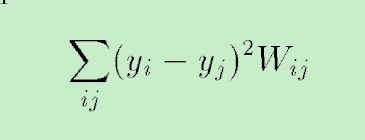
其中W是原始空间中,点x之间的权值,如果点越近,则相应的权值W越大,y是降维之后空间的点。这个公式就保证了降维后,点之间的位置关系与原空间的位置关系尽量一致。进而有如下的推导,
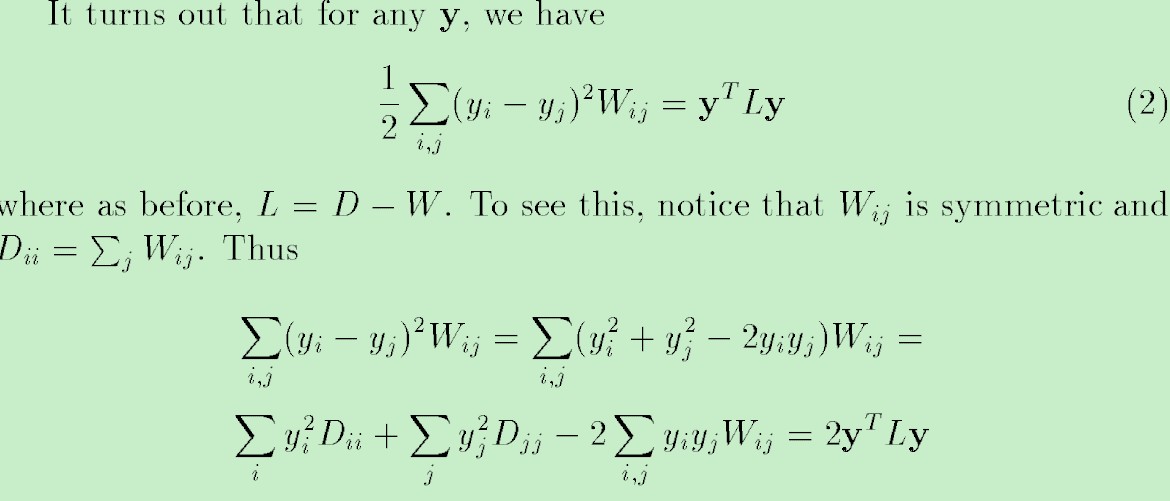
理解上面的推导你需要知道:
$D_{ii}$和$D_{jj}$分别是W的每行和每列元素和的对角矩阵,由于W是对称矩阵,所以Dii与Djj相等。
线性代数里的二次型,y’Wy的展开式。
最后我们的问题就转化为优化f’Lf,L就是大名鼎鼎的Graph Laplacian,这个式子有诸多特点,如最小的特征值为零,并且对应的特征向量正好为1(根据D-W计算的性质可以得到)。具体求这个这个式子f’Lf的最优解,可以根据Rayleigh quotient来求。它的最大值和最小值分别等于矩阵A的最大的那个特征值和最小的那个特征值,并且极值在x等于对应的特征向量时取到。由于f’f是常数,因此最小化f’Lf实际上也就等价于最小化R(L,f)。(如何转化为Generalized eigenvector问题)
Spectral Clustering问题是聚类问题,聚类问题其实和图分割问题是等价的,把数据聚合成几个类,就等价于把图最小割成几个子图。由于图的最小割是NP问题,我们首先设
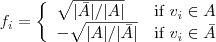
那么对于一个图来说,把f的值带入上面的式子
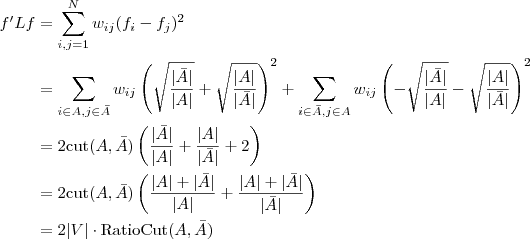
我们发现最小割的问题也是优化f’Lf这个式子,只不过优化时加了限制条件,就是f只能取两个值。
这里的求得的f是特征向量,所有特征向量就是我们聚类的结果,发现这个和Laplacian Eigenmap降维的结果是一样的,而不一样的是,对于聚类后的结果,特征向量f只有两个值(聚成两类的情况)。如果要聚成k个类,对于特征向量f进行knn聚类就可以了。
其实我这篇文写的毫无意义,如果想去了解Spectral Clustering等,建议认真去读下面的参考文章,作者写的非常详细认真。
参考文章
漫谈 Clustering (4): Spectral Clustering
漫谈 Clustering (番外篇): Dimensionality Reduction