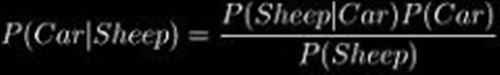
10月转眼之间就过了,时间过的太快了,而我在十月净瞎忙,写篇博客的时间都没有,终于等到了11月第一个周末,才终于给自己找了个时间。
第一个问题是那个三门问题,以前在博弈论相关的书上看到过,后来便只记得答案了。现在看贝叶斯相关的东西,顺便拿出来复习下:
三门问题:参赛者会看见三扇关闭了的门,其中一扇的后面有一辆车,当参赛者选择一扇门后,节目主持人会开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门是否会增加参赛者赢得汽车的机率?
我们来看使用普通的条件概率来解决这个问题,我们定义C事件为参赛者打开这个门选择到一个车,定义S事件为主持人打开另一扇门选择一只羊,则
C事件:参赛者选中一个车。那么P(C)=1/3
S事件:主持人选中一个羊。那么P(S)=1
由于主持人始终知道哪个门后有羊,所以选择羊的概率是1。
那么我们要求的就是P(C/S),也就是在主持人选择一只羊之后,参赛者选择到车的概率,而P(C/S)=P(C∩S)/P(S)。
所以关键在于求P(C∩S),即参赛者选中一个车时,主持人选中一个羊的概率。下图是所有选择的可能:
| 参赛者 | 主持人 | |
| 车 | 羊 | 羊 |
| 羊 | 车 | 羊 |
| 羊 | 羊 | 车 |
有图可知, P(C∩S ) =1/3
则 P(C/S)=P(C∩S )/P(S) =1/3
此时我们发现当主持人打开这个门后,选择到一个车概率仍然是1/3。和之前没有变化,可是如果这时参赛者换另一扇门那么选择到车概率就是2/3了,中奖的概率是以前的两倍。
其实之所以提出这个问题,是因为这个问题是标准的先验概率和后验概率的问题,也就是新
的事件发生后对先验概率的影响,所以用贝叶斯公式解这个题是最方便了。
贝叶斯解法:
如果用P(Car)代表你刚开始选中的门里有车的概率,用P(Sheep)代表主持人打开的门里是羊的概率,用|表示条件概率,那么由Bayes公式有:
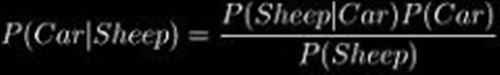
| 其中P(Sheep | Car)表示在你选中了车的条件下,主持人打开的门里是羊的概率,概率显然是1。由前面的假设也显然有P(Car)=1/3,而P(Sheep)=1,所以直接求得 P(Car | Sheep)为1/3。即新事件对先验概率没有影响,仍然是1/3,如果此时参赛者换了另一个门的话,则选到车会变成2/3。 |
第二个问题是室友提出的一个有关relatively prime问题,
任取两个自然数,它们互素的概率是多少?
首先设任意两个自然数为a、b,它们互素的概率为p,设一自然数k,则k为a、b的公因子的概率为1/k^2 (k是a因子的概率是1/k,则k同时是a,b公因子的概率是1/k^2 。)
令a=m*k ,b=n*k ,则“m、n互素”的充分必要条件为“k是a、b的最大公因子”。(如果k不是a,b最大的公因子,则m,n必然还有其他的非1公因子,则m,n不互素)。
| 由于在k是a、b的公因子的前提下,m、n也等价于两个任意自然数,所以它们互素的概率也为p,即在k是a、b公因子的前提下,k是a、b最大公因子的概率为p。由于k不是a、b公因子的情况下,k是最大公因子的概率为零。所以根据全概率公式(P(A)=P(A | B1)*P(B1) + P(A | B2)*P(B2) + … + P(A | Bn)*P(Bn)),k是a、b最大公因子的总概率就为: |
P{k是a、b公因子}*P{k是a、b最大公因子/k是a、b公因子}=p/k^2 。
对于事件k是a、b最大公因子来说,任何两个自然数,必然存在最大公因子,我们需要做的穷举所有自然数即可(可以这样理解,只有一个数是最大公因子,它的概率是1,其他的数是最大公因子的概率都是0,所有数的概率加起来肯定还是1),所以有
\begin{equation} \sum_{k=1,2,3…}\frac{p}{k^2}=1\end{equation}
求解得p等于6/π^2)(这里涉及到p级数的求和,方法是对一个周期函数展开成傅里叶级数形式,可以求得奇数项的和为π^2/8,进而求得自然数的和为π^2/6,具体参考高等数学教科书)。
这个题还有另一种解法
设任意两个自然数m,n,pk为所有素数的集合。一个自然数有因子pk的概率为1/pk 。m,n同时有因子pk的概率为1/pk^2 ,所以m,n不同时有因子pk的概率为1-(1/pk^2) 。m,n互素就是说,对于所有k=1,2,3……,m,n不同时有因子pk(这里k的含义是第几个素数,而pk就是那个相应的素数)。显然,这个概率为: \begin{equation} \prod_{k=1,2,3..}1-\frac{1}{pk^2}\end{equation} 由于k一直取到无穷大,所以就是对连乘式取极限。根据Euler_product_formula,则这个极限的倒数,等价于求$\sum_{k=1,2,3…}\frac{1}{k^2}$ 。这个连加的结果是π^2/6,所以所求概率为6/π^2 。
这里运用一个公式Euler_product_formula这个公式的证明也很有意思,具体可以看wiki。

解到这里,你可能会疑惑,上面为什么一定要用素数pk呢,能不能用自然数呢,即两个数为互素数的充要条件是,它们不同时有所有质数的公因子。能不能是它们不同时拥有所有自然数的公因子呢,这样算的话,概率是不是会变大?
其实概率不会变的。当然可以改成“不同时拥有所有自然数的公因子的两个数是互素数”,因为这个也是充要条件。但是这时候各个概率就不是独立的了,不能简单相乘相加。比如“拥有(或者不拥有)公因子2”和“拥有(或者不拥有)公因子4”两个事件不是独立的,而应该变成“拥有公因子2但没有公因子4”和“拥有公因子4”,这两个概率加起来,跟“拥有公因子2”就没有区别了。
第三个题是google 2012校招的笔试题,
从-2到2之间,任意取两个数,这个两个数之和大于1的概率是多少?
我们定义一个二维的参数空间,其中任意一点(x,y)表示我们的一个解,如图
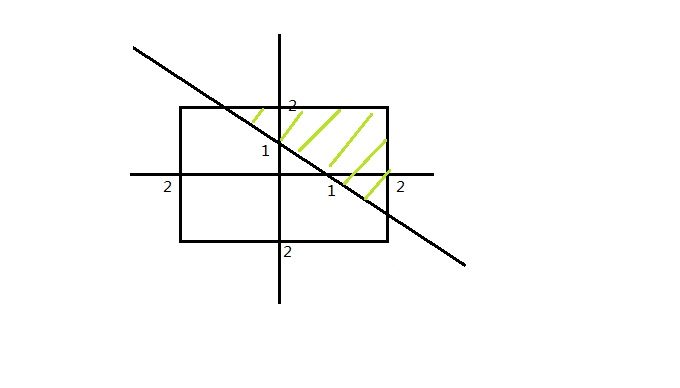
这个数之和则可以用函数z=x+y表示,题目是大于1,则函数是x+y>1。则两个数之和大于1的概率是阴影面积除以总的解空间的面积,使用小学数学知识,得9/32。
解完这个题后,又有人提出了一个类似的题目,对于任意一根棍子,随机找两个点将棍子分成三段,这三段能组成三角形的概率是多少?
这道题被我秒解。过程如下: 设任意两段棍子为x和y,滚在总长度为a则 a/2>x>0,a/2>y>0,a>x+y 则根据三角形的两条边和大于第三边得, x+y>a-x-y即x+y>a/2 将这四个不等式放在坐标空间就是
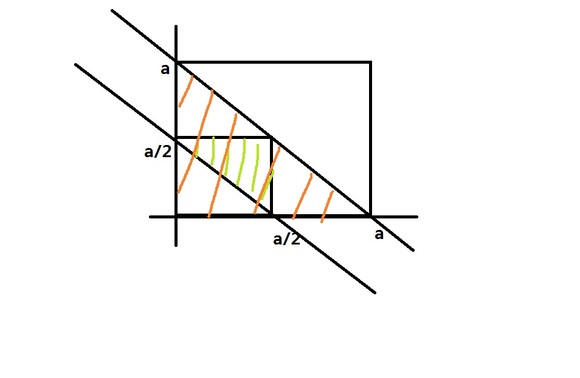
青色的阴影面积就是所有x,y可以组成三角形的区域,组成的面积是a^2/8。 再看x和y所有能取到的值的集合,其实是 a>x+y 所限定的区域,是红棕色的阴影面积,即a^2/2两者相除,得到这三段能组成三角形的概率是1/4。
参考资料:
http://www.ruanyifeng.com/blog/2011/08/bayesian_inference_part_one.html