大学时，我们学习高等数学，线性代数，概率统计等等数学科目，可是从来没有想过这些知识能有什么用，或许这已经成为了一种习惯，所有的上课时学习的知识在考试后好像都没有用处了。然而，终于有一天，当我在读文章的时候，看到作者使用特征值来解释一些问题，这时，才发现自己已经将以前的知识忘的干干净净，即使当我重新拿起来书复习以前的知识后，仍然不能理解，为什么使用特征值就能解决这个问题，为什么要使用特征值，特征值是什么，它到底有什么用处。
让我们先来复习下特征值和特征向量的知识。 定义设A是n阶矩阵，若存在数及非零向量X，使得$AX=\lambda X,X≠0$则称是A的特征值，X是矩阵A属于特征值的特征向量。计算特征值的方法常由特征多项式|E-A|=0来求，求得后，带入原式便可求得特征向量。
具体例子可以参考这里。那么为什么要求特征值和特征向量呢，它有什么几何意义？观察$AX=\lambda X$会发现，矩阵A乘以向量X其实就是进行一次几何变换，这里A乘以X变换之后结果仍是X方向的向量，不同的只是长度上的伸缩。那么我们就可以这样认为，A乘以特征向量X之后，结果就是A在特征向量X上的投影。鉴于一个矩阵我们往往能求得不只一个特征向量，我们可以这样理解，其本质就是把矩阵A所代表的空间，进行正交分解，使得A的向量集合可以表示为每个向量在各个特征向量上面的投影，而特征值就投影的权重。就像我们在二维空间里分析几何问题，尝尝投影到x,y轴上一样，同样的道理。
下面我们来看一个具体的例子，边角检测（Harris Detector）
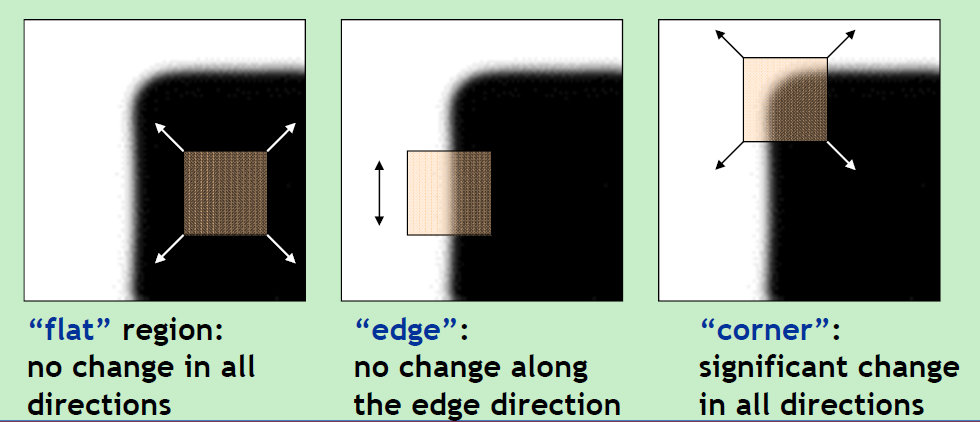
什么叫角点呢，首先看上面面这个图，Harris检测的理论依据就是在一个角点，它向各个方向移动时，intensity 改变最大。根据此理论理解下面的公式推导，便很容易了。
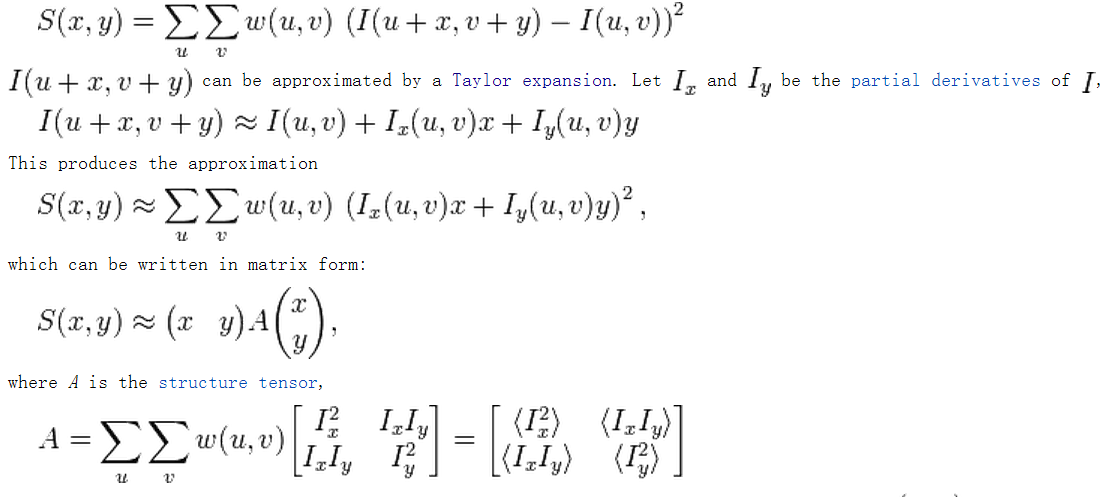从而得到一个2*2的矩阵，然后分析这个矩阵的特征值就可以推断这里是否一个角点了。那么关键是，为什么要分析这个矩阵的特征值呢？我的理解是，这个矩阵的第一项是x轴方向的导数，第四项是y轴方向的倒数，第二项和第三项分别是xy轴上的导数。那么我们可以把这个矩阵往x和y轴方向上投影，看他们在这两个方向上的变化。具体做法是把这个矩阵进行变换，求其在两个方向的特征向量，而特征值就是其权值。
最后根据角点的特性，如果在x和y轴的变化都很大，则是一个角点，如果在一个方向上变化为零，则是一条边，如果在两个方向变化都为零，则是普通区域。
再来看一个凡是提到特征值都会提到的PCA（Principle Component Analysis），PCA方法就是把数据降维，把原来多维的数据投影到几个维度上，然后保留那些最突出的数据（方差最大），因为这些数据包含了整个数据的最重要的信息。看下面这个图，当把这些点投影到x和y轴上后，很明显投影到y轴上的数据几乎都差不多，没有什么用，而投影到x轴的数据差别比较大，体现了这些数据的主要信息，所以要保留这些数据。
理解了它的原理后，我们来具体看一下PCA的计算过程。
获取数据$P_1,P_2,…,P_n$（每一个数据为一个m维列向量）。
求出数据平均值$M=M=\frac{1}{n}\sum^n_{i=1}P_i$，并用原数据减去均值得到$P_i^{‘}= P_i-M$。
计算协方差矩阵$Cov=\frac{1}{n}\sum^n_{i=1}(P_i^{‘},P_i^{‘T})$。
计算协方差矩阵的特征值$E_1,E_2,…E_m$与特征向量$EV_1,EV_2,…EV_m$特征值与特征向量成对出现）。
由大到小依次排列特征值得$E_1^{‘},E_2^{‘},…E_m^{‘}$，对应特征向量为$EV_1^{‘},EV_2^{‘},…EV_m^{‘}$。特征向量代表了原数据的分布方向，其对应的特征值越大，则该向量越重要（即为主元）；其对应的特征值越小，则该向量越次要。
这里又出现了一个重要的概念，协方差，不知道的大家可以参考这里。说的简单的，比如说一个妹子的胸很大，那么我们想知道到底大到什么程序，就可以使用方差来描述，方差越大表示她比普通女生的胸越大。有时候，我们还想知道女生的胸的大小和受欢迎程序的关系，就需要协方差，用X来表示女生的胸的大小，用Y表示女生的受欢迎程度，那么协方差就是 \begin{equation} cov(X,Y)=\frac{\sum_{i=1}^n (X_{i}-\bar{X})(Y_{i}-\bar{Y})}{n-1} \end{equation}
如果结果是正值，那么说明这两者是正比关系，就是女生胸越大则越受欢迎，反之则是反比关系。如果结果等于0，说明两者是独立的，没有关系，当然这种情况现实中不可能发生，囧。
好了，言归正题，这里之所以要计算协方差主要是因为我们需要保留差别最大的数据，而协方差正好是两两之间的关系，计算完之后得到协方差矩阵，我们需要降维了，所谓的降维就是把矩阵投影到各个特征向量上去，然后比较各个特征值，保留特征值大的数据，也就是方差最大的数据，正是我们需要的最有特征的数据，然后在求得相应的特征向量，即是我们所需要的主成分。
使用时，就是把数据投影到主成分上，然后和标准值进行相减，如果结果落在阀值内就说明是属于这一类，反之则不属于。
参考文章：
http://www.douban.com/group/topic/23708138/
http://en.wikipedia.org/wiki/Corner_detection#The_Harris_.26Stephens.2F_Plessey_.2F_Shi-Tomasi_corner_detection_algorithm
http://en.wikipedia.org/wiki/Harris_affine_region_detector